Множественная регрессия

Поиск в руководстве по статистике Интернета

Общая цель

Общая цель множественной регрессии (этот термин был впервые использован Пирсоном в 1908 году) - это количественная оценка отношений между многими независимыми переменными (в том числе) и переменной зависимостью (критериальная, обьянская). Например, агент по торговле недвижимостью (агент) собирает данные о зданиях - площадь (в м2), количество спален, средний доход жителей района и субъективную оценку привлекательности объекта. Если у вас уже есть такие базы данных, у вас может возникнуть соблазн ответить на следующий вопрос: Как отдельные размеры влияют на цену здания? Таким образом, можно обнаружить, например, что количество спален, чтобы лучше покрыть цену здания, например, насколько приятно это выглядит на основе привлекательной оценки (субъективная привлекательность). Вы также можете обнаружить объекты "окраины", то есть здания, которые имеют большую ценность, чем это получается из данных, собранных агентом.

Аналитики - специалисты по управлению персоналом обычно используют множественную регрессию для оценки размера вознаграждения. Для этой цели можно определить ряд факторов, таких как, например, «сфера ответственности» (редакция) и «незаявленные числа» ( L_podw ), от которых можно предположить, что ценность работы зависит от них. Затем специалист по управлению персоналом проводит собеседование в аналогичных компаниях, где записывает высокую заработную плату и соответствующие характеристики для разных рабочих мест. Такая информация может затем использоваться для создания уравнения множественной регрессии в форме (примерной форме):

Заработная плата = 0,5 * A + 0,8 * L_podw

Имея такой подход, аналитик теперь может легко построить прогнозируемый график заработка на основе этого уравнения в зависимости от заработка на соответствующих должностях в рассматриваемой работе. Такой график позволяет легко определить, какие задания недооценены (точки будут ниже линии регрессии), которые пересмотрены (выше линии регрессии) и которые вознаграждены в соответствии с тенденцией.

В социальных и естественных науках анализ множественной регрессии широко используется в качестве инструмента исследования. Вообще говоря, множественная регрессия позволяет исследователю ответить на вопрос: «Какой размер лучше всего описать ...». В педагогических исследованиях вы можете, например, задать вопрос: каковы наилучшие характеристики (давайте предскажем наименьшее) для успеха в старшей школе? Психолог может задать вопрос: какая личностная черта лучше всего описывает предрасположенность социальной адаптации? Социологи, в свою очередь, могут захотеть узнать, какой из многих социальных показателей лучше всего подходит для составления прогноза по приспособляемости новой группы иммигрантов?

Смотрите также Техники добычи данных (data mining) и главы: Общие регрессионные модели и Общие линейные модели ,

Расчетный подход

Общая вычислительная проблема, которая должна быть решена в множественном регрессионном анализе, состоит в сопоставлении прямой линии с набором точек.

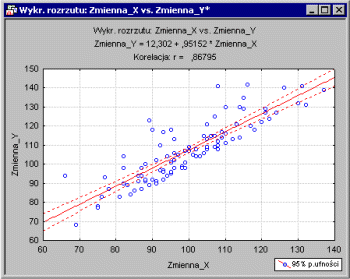
В простейшем случае - одна зависимость переменной и одна независимая переменная - вы можете проиллюстрировать это точечная диаграмма ,

Смотрите также Методы добычи данных (data mining) и Общие регрессионные модели и Общие линейные модели ,

Метод наименьших квадратов. На графике рассеяния мы представляем независимую переменную X и переменную зависимость Y. Эти переменные могут быть представлены, например, с помощью Интеллектуальной квоты (IQ), измеренной с использованием соответствующего теста, и результатов успеваемости в школе (средний балл, O). Каждая точка на графике представляет одного учащегося, то есть его IQ и O. Цель процедуры линейной регрессии - сопоставить линию с этими точками. Программа будет соответствовать линии так, чтобы сумма квадратов точек расстояния на диаграмме рассеяния от линии регрессии была минимальной. Благодаря этому свойству эту общую процедуру иногда называют методами оценки наименьших квадратов (см. Также описание методы наименьших квадратов ).

Смотрите также Методы добычи данных (data mining) и Общие регрессионные модели и Общие линейные модели ,

Регрессия регрессия. Прямая в двумерном пространстве (на пасти) определяется уравнением Y = a + b * X. Это означает, что значение переменной Y можно рассчитать как сумму константы ( а ) и произведения наклона ( b ) на переменную X. Эквивалент по константе также называется свободным выражением , а наклон - это либо коэффициент регрессии, либо коэффициент B. Например, O можно рассчитать как 1 + 0,02 * IQ . Таким образом, IQ = 130 известен для интеллекта IQ , и мы прогнозируем его среднее значение O = 3,6 (потому что 1 + 0,02 * 130 = 3,6).

Например, следующая анимация показывает регрессию регрессии в двумерном пространстве, выделенную для трех различных доверительных интервалов (90%, 95% и 99%).

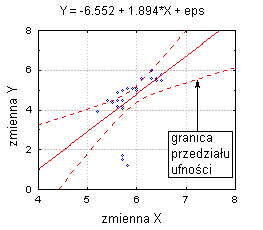
В многомерном случае, когда существует более одной независимой переменной, линия регрессии не может быть так визуально изображена в двумерном пространстве, но мы получим ее одинаково прямой. Например, если помимо IQ у нас все еще есть другие предикторы (например, уровень мотивации , уровень внутренней дисциплины ), мы могли бы построить линейное уравнение, содержащее все эти переменные. В общем, множественность множественной регрессии имеет вид:

Y = a + b1 * X1 + b2 * X2 + ... + bp * Xp

Однозначный прогноз и частичная корреляция. Отметим, что в этом случае коэффициенты регрессии (коэффициенты B ) представляют собой независимые входные данные каждой из независимых переменных для прогнозирования зависимой переменной. Другим способом выражения этого факта является следующая формулировка: переменная Xi коррелируется с переменной Y после учета влияния всех других независимых переменных. Этот вид корреляции называется корреляцией частиц (этот термин был впервые использован Йоль в 1907 году). Давайте возьмем это на примере. Если он выполнил соответствующие тесты, мы, вероятно, получили значительную отрицательную корреляцию между длиной восков и увеличением популяции (то есть, чем меньше индивидуум душ волос). На первый взгляд это кажется странным. Однако, если мы добавим новую переменную Pe в уравнение регрессии, то эта корреляция, вероятно, исчезнет. Это было бы потому, что женщины, в среднем, имеют души волос, чем мужчины, и меньше, чем мужчины. Таким образом, если мы устраняем различия, вводя переменную Pe в уравнение, то связь между длиной восков и ростом исчезнет, ​​потому что длинный воск не будет больше способствовать росту, чем то, что добавляет к нему переменная Pe (и больше не wosw). ). Другими словами, после учета переменной Pe частотная корреляция между увеличением и длиной wosw становится равной нулю.

Прогнозируемые значения и остаточные значения. Линия регрессии выражает наилучший прогноз зависимой переменной ( Y ) для данных независимых переменных ( X ). Однако природа редко (если вообще) предсказуема идеально, и обычно у нас есть отклонения точек измерения от линии регрессии (как можно убедиться на графике рассеяния). Отклонение данной точки на графике от линии регрессии (то есть от ее прогнозируемого значения) называется остаточной величиной.

Остаточная дисперсия и R-квадрат. Чем меньше дисперсия остаточных значений в линии регрессии по отношению к общему отклонению, тем лучше прогноз. Если, например, не будет никакой связи между переменными X и Y , то отношение остаточной переменной Y к общей волатильности будет равно 1,0. Если бы X и Y были сильными (в смысле функциональных отношений) зависимыми друг от друга, то остаточная изменчивость была бы равна нулю, а такое соотношение было бы 0,0. Наиболее часто обсуждаемый размер находится между этими крайними значениями, то есть между нулем и единицей. Высоко определенное как 1 минус это отношение называют R-квадратом или определяющим фактором . Это имеет следующую интерпретацию. Если, скажем, значение R-квадрата равно 0,4, то будет известно, что дисперсия значения Y в линии регрессии в 1-0,4 раза превышает исходную дисперсию Y. Другими словами, 40% исходного Y- отклонения было переведено регрессией, а 60% осталось в остаточной волатильности. В идеальном случае я хотел бы объяснить как можно больше (если не все) исходного варианта. Значение R-квадрата является показателем качества соответствия модели данным ( R-квадрат, близкий к 1,0, указывает, что почти все переменные зависимой переменной могут быть выделены независимыми переменными, включенными в модель).

Интерпретация коэффициента корреляции R. Обычно скорость, с которой две или более инцидентных переменных (независимых или X ) связаны с дисперсией дисперсий (зависимой переменной Y ), выражается значением коэффициента корреляции R , определенного как квадратный корень из R-квадрата . При множественной регрессии R может принимать значения от 0 до 1. Чтобы определить направление зависимости от конкретной переменной, следует использовать значение коэффициента регрессии ( B ). Если B положительный, то отношение положительное (с увеличением X значение Y возрастает: например, чем выше IQ IQ, тем выше средний рейтинг O), если B отрицательное, отношение отрицательное (например, чем меньше число класс, лучшие результаты теста). Конечно, если значение B равно нулю, то между переменными нет никакой связи.

Отношения, ограничения, практические соображения

Установление лайнерства. Прежде всего, поскольку оно вытекает из самого имени, множественная линейная регрессия требует предположения, что отношение между переменными является линейным. На практике засуху такой идеи практически невозможно доказать, но в итоге процедуры множественной регрессии устойчивы к небольшим отклонениям от этого ожидания. Всегда стоит правило следует анализировать под этим двумерным углом точечные диаграммы изученных переменных. Если связь нелинейная, вы можете либо преобразовать переменные, либо явно применить нелинейные компоненты.

Предположение о нормальности. При множественной регрессии предполагается, что остальные (различия между наблюдаемыми и рассчитанными значениями из уравнения регрессии) подчиняются нормальному распределению. И, тем не менее, хотя большинство тестов (в частности, тест F ) устойчивы к отклонениям от этого ожидания, перед окончательными выводами всегда целесообразно увидеть основные переменные, которые являются предметом нашего интереса. Мы можем создавать гистограммы и диаграммы нормальности для остатков.

Ограничения. Основным методологическим ограничением, лежащим в основе всех методов регрессии, является тот факт, что с их помощью вы можете только убедиться в существовании отношений , но вы не можете обнаружить, что есть причинно-следственная связь, которая является основой этих отношений. Вы можете, например, доказать существование тесной взаимосвязи (корреляции) между ущербом, причиненным пожаром, и количеством пожарных, принимающих участие в пожаротушении. Разрешает ли это нам прийти к выводу, что пожарные причиняют ущерб? Конечно нет. Вероятным объяснением наблюдаемой взаимосвязи является тот факт, что чем больше пожар (переменная, которую мы не включили в наш анализ), тем больше количество всплесков (в общем) участвует в его тушении. Несмотря на очевидность этого примера, в реальных ситуациях часто упускается из виду, что такие соображения следует учитывать.

Выбор количества переменных. Множественная регрессия - это обманчивый метод, достаточно «ввести» достаточно переменных, и обычно для некоторых из них вы найдете важные. Это связано с тем, что считается статистически значимым случайное воздействие, учитывая достаточно большой набор потенциальных предикторов. Этот эффект чаще всего усиливается в случаях, когда наблюдается небольшое количество наблюдений. Интуитивно очевидно, что из анкет, содержащих 100 вопросов, заполненных 10 респондентами, трудно сделать разумные выводы. Многие авторы рекомендуют анализировать как минимум в 10-20 раз больше случаев (наблюдения, измерения, респонденты), чем есть переменные (запросы). В противном случае оценки по линии регрессии будут очень нестабильными и будут сильно изменяться по мере увеличения числа случаев.

Платина и кондиционирование матрицы. Это типичная проблема во многих случаях корреляционного анализа. Мы представляем, что у нас есть две переменные, которые учитывают рост человека (независимые переменные X ): (1) вес в килограммах и (2) вес в декаграммах. Конечно, эти две переменные явно избыточны. Вес, независимо от того, в каких единицах он выражен, является одной и той же переменной. Учитывая, какая из этих переменных является лучшим предиктором роста, будет деятельность, связанная с эго. Однако такую ​​проблему пришлось бы решать, если бы мы столкнулись с задачей множественной регрессии, при которой изменение зависимости ( Y ) будет увеличиваться, и независимыми переменными ( X ) двух вышеупомянутых мер гравитации. В случаях, когда существует много переменных, проблема обусловленности не всегда сразу очевидна. Иногда это можно увидеть только тогда, когда в уравнении регрессии много переменных. Тем не менее, когда это раскрывается, это почти всегда означает, что мы имеем дело с набором независимых переменных, связанных друг с другом (избыточный набор независимых переменных - одна или несколько переменных могут быть выражены другими). Существует ряд статистических показателей для выявления этого типа избыточности (допуски, полуциклические R и т. Д.), А также несколько профилактических мер (например, дорсальная регрессия ).

Соответствующие полиномиально центрированные модели. Корректировка полиномов более высокого порядка для независимой переменной, среднее значение которой отличается от нуля, может вызвать проблемы сложности. В частности, многочлены будут сильно коррелированы из-за среднего значения исходной независимой переменной. В случае больших чисел эта проблема очень серьезна, и если вы не примете соответствующие контрмеры, это может привести к неверным результатам! Решение этой проблемы заключается в «центрировании» независимой переменной (иногда эти процедуры называются «центрированными полиномами»), т. Е. В среднем вычитании, а затем в вычислении полиномов. Подробное описание этой проблемы (и, например, анализ полиномиальных моделей) можно найти в классическом учебнике Neter, Wasserman and Kutner, 1985, в главе 9.

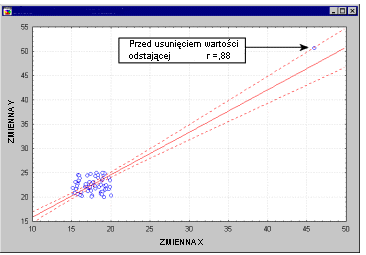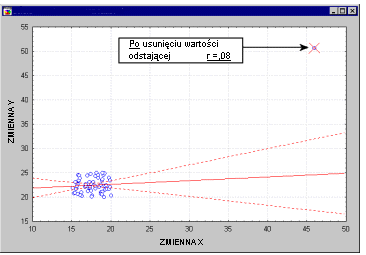
Важность остаточного анализа. Хотя большинство связанных с регрессом правил не может быть проверено напрямую, могут быть обнаружены серьезные разногласия с ними, и их следует рассматривать соответствующим образом. В частности, прямые наблюдения (т.е. экстремальные случаи) могут серьезно нарушить результаты, «притягивая» или «сдвигая» линию регрессии, в каком направлении вызваны изменения коэффициентов регрессии. Иногда, удалив только одну отдаленную точку, вы можете получить совершенно разные результаты анализа.