Тесты на значимость различий для независимых выборок

В медицинских исследованиях наиболее распространенной статистической проблемой является сравнение двух групп населения по одному признаку или двум признакам. Методы таких сравнений можно разделить на две группы:

• сравнение определенных параметров популяции (средние значения, стандартные отклонения) - тогда обычно используются параметрические тесты;
  
• сравнение некоторых характеристик, которые не являются параметрами (например, форма распределения) - в таких случаях обычно используются непараметрические тесты.

Хотя этот параметр является более востребованной и важной характеристикой как населения, так и отдельных лиц, его отсутствие не заставляет нас отказываться от статистических исследований.

В медицине и биологии исследования часто сравнивают значения двух или нескольких средних значений. Поэтому следующие несколько эпизодов цикла будут посвящены этой проблеме.

Позвольте мне начать с проверки различий между средними значениями двух попыток. Эти тесты подтверждают нулевую гипотезу о равенстве средних в двух группах.

Предположим, мы даем две снотворные для двух разных групп (18 человек из группы А и 24 человека из группы В). В таблице 1 показана продолжительность сна (в минутах) людей после введения препарата.

SEN_A 438 154 374 250 145 299 404 412 313 215 216 304 234 302 234 302 123 298 107 115 SEN_B 416 454 400 315 373 370 203 372 249 275 339 439 262 372 262 372 249 275 352 320 392 263 379 309 505 310

Мы ищем ответ на вопрос, какой из этих препаратов более эффективен. Чтобы решить такие проблемы, мы используем тесты на различия между средними двумя образцами для несвязанных переменных; чаще всего это t- студенческие тесты на несвязанные переменные . Их также можно использовать для оценки конкретной разницы между группой пациентов, принимающих исследуемый препарат, и группой пациентов, получающих плацебо; Затем мы рассмотрим две группы: контрольную и экспериментальную.

Предположим теперь, что в группе людей мы тестируем кровяное давление до и после приема лекарств. Мы спрашиваем, вызывает ли этот препарат значительное падение давления. На этот раз у нас есть две серии измерений, относящихся к одному и тому же образцу (т.е. в одной и той же группе, до и после введения препарата), и мы хотим проверить гипотезу о среднем размере различий между полученными результатами. Первая серия данных - это результаты измерения исследуемого признака (давления) в один момент времени (до приема препарата), вторая - результаты измерения того же признака у одного и того же человека во втором моменте времени (после приема препарата). Для задач этого типа мы используем t- студенческие тесты для связанных переменных .

Позвольте мне начать с основных предположений о тестах t- студента:

1. Принцип рандомизации

Если мы хотим обобщить выводы исследования, мы должны гарантировать репрезентативность выборки для населения. Это возможно только при случайном выборе образца ( первое правило рандомизации ). Если этот принцип не соблюдается, сделанные выводы применимы только к пациентам из данной больницы, лицам, принадлежащим к определенной возрастной группе или данному полу и т. Д.

Исследования по оценке эффективности нового лекарства или лечения должны проводиться как минимум в двух эквивалентных группах людей, чтобы проверить новое лекарство по сравнению с предыдущим (или плацебо). Решение о том, какое лекарство получает человек, принимается случайным образом ( второе правило рандомизации ). Если второе правило рандомизации не соблюдается, фактор выбора может оказать большое влияние на различия между средними значениями переменной и, как следствие, могут быть сделаны неверные выводы.

2. Предположение о нормальности распределения переменных

Существуют специальные статистические тесты, чтобы оценить, является ли данное эмпирическое распределение нормальным - они обсуждались в предыдущем эпизоде.

3. Предположение об однородности дисперсии

F- критерий, критерий Левена или критерий Бартлетта используются для проверки этого предположения. Если эти тесты не показывают однородности дисперсии, следует использовать тест Корана и Кокса.

В дополнение к вышеприведенным предположениям мы также должны учитывать тип сравнения . Тесты серьезности различий делятся на два подмножества:

• тесты для независимых групп (то есть для несвязанных переменных)
  Эти тесты сравнивают среднее значение тестируемой переменной для двух групп одинаковых или разных чисел (обычно это контрольная и экспериментальная группы).
• тесты для зависимых групп (то есть для связанных переменных)
  Эти тесты используются для сравнения средних значений данной переменной в одной и той же группе, но тестируются дважды по времени (например, продолжительность сна до и после приема препарата).

В зависимости от проблемы, которую вы рассматриваете, вы должны выбрать соответствующий тест. В этом эпизоде ​​я буду обсуждать тесты для несвязанных переменных. Рисунок 1 представлен алгоритм выбора такого теста.

Как вы можете видеть, в дополнение к вышеупомянутым предположениям о выборе теста, размер группы также определяет. В статистической литературе значение 30 определяется как пограничная популяция. Многие тесты также имеют свои ограничения на минимальный размер сравниваемых групп, а некоторые - несколько вариантов для групп разных размеров.

Для дальнейшего рассмотрения предположим, что наблюдаемые переменные имеют нормальное распределение в двух сообществах; как поступить в обратном случае - об этом в следующем эпизоде.

В настоящее время, когда у нас есть компьютер, никто не проверяет гипотезу «пешком». Мы используем различные статистические пакеты (например, BMDP, SAS, SPSS, STATGRAPHICS, STATISTICA), которые также «выбирают» правильный тест в зависимости от размера выборки. Ниже я привожу пример анализа с использованием программы STATISTICA, опуская математическую форму отдельных тестов, и наиболее интересные графические интерпретации полученных результатов.

В STATISTICA для проверки различий между средними значениями двух несвязанных выборок используйте параметр « t- критерий для независимых выборок » в модуле «Базовая статистика и таблицы». Проверка с и проверка t происходят в программе STATISTICA под общим названием t test. Сама программа выбирает соответствующий тест для данного числа. Тест Корана и Кокса - это t- тест в STATISTICA с отдельной оценкой дисперсии.

Для наших образцов данных (таблица 1) мы получим следующий лист результатов ( рисунок 2 ):

Нумерованные поля в таблице результатов (наиболее важные для интерпретации) означают:

[1], [2] средние значения в первой и второй группе
[3] значение t- критерия (при условии предположения однородности дисперсии)
[4] Уровень значимости рассчитывается с помощью компьютера.
[5] Значение t- критерия для гетерогенных дисперсий (так называемый критерий Кокрана и Кокса)
[6] компьютерный уровень вероятности t-критерия для разнородных дисперсий
[7], [8] номера первой и второй групп
[9] стандартное отклонение в первой группе
[10] стандартное отклонение во второй группе
[11] Значение F теста для проверки однородности дисперсии
[12] компьютерно-вычисленный уровень значимости F- теста на однородность дисперсии
[13] Значение теста Левена для проверки однородности дисперсии
[14] Уровень значимости Левена, рассчитанный компьютером для однородности дисперсии
[15] Значение критерия Брауна и Форсайта, проверяющее однородность дисперсии
[16] компьютерный уровень вероятности критерия Брауна и Форсайта для однородности дисперсии

Примечание: поля [5] и [6] появляются, когда в окне «Параметры» (рисунок 3) мы выбрали t- тест для неоднородных дисперсий, поля [13] - [16] и когда мы выбрали тест Левена и тест Брауна и Форсайта за однородность дисперсии.

Рис. 3

Как не заблудиться в зарослях полученных результатов? На что обратить особое внимание?

Мы начнем с проверки последнего оставленного нами предположения - предположения о равномерности дисперсии. Нулевая гипотеза, которую мы хотим проверить, предполагает однородность (равенство) дисперсии. Есть 3 теста, подтверждающих эту гипотезу - тест F , Левена и тест Брауна и Форсайта. Последний пользуется лучшим мнением. Рассчитанные значения этих тестов отображаются в полях с номерами [11], [13] и [15]. Уровни значимости, связанные с этими тестами, можно найти в полях с номерами [12], [14] и [16] соответственно. Как видно, для данных в нашем примере p для всех трех тестов превышает 0,05. Нет оснований отвергать нулевую гипотезу об однородности дисперсии, и можно предположить, что это предположение выполнено. В этой ситуации значения соответствующего t- критерия для однородных дисперсий ищутся в поле [3] и соответствующий уровень значимости в поле [4]. Из них следует, что нулевая гипотеза о равенстве средней продолжительности сна должна быть отвергнута. Таким образом, средняя продолжительность сна после приема препарата A значительно отличается от среднего времени сна после приема препарата B. Можно сделать вывод (на основе средних значений), что препарат B более эффективен, чем препарат A, при уровне значимости 0,05 или даже меньше. (р = 0,0062).

Если предположение об однородности дисперсии значения t- критерия не выполняется, мы ищем так называемые Тест Кокрана и Кокса в поле [5] и соответствующий уровень значимости p в поле [6].

На фиг.4 представлена ​​графическая интерпретация результатов, полученных в виде так называемых коробки с усами.

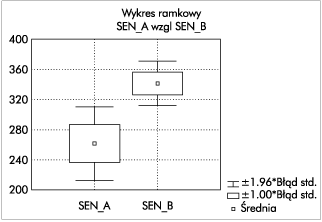
Рис. 4. Диаграмма "коробка с усами" - первый пример

Эта графическая форма обсуждалась в предыдущем эпизоде. Средний квадрат представляет среднее значение, а усы определяют 95% доверительный интервал данного среднего. Гипотеза о равенстве сред может быть отвергнута, когда усы ящиков не перекрываются (как на этом рисунке).

В качестве второго примера рассмотрим средний уровень сальсолина для женщин и мужчин с определенным заболеванием. В таблице 2 приведены результаты измерений для 32 человек.

Сальсолин 139,8 118,8 157,5 96,1 99,5 98,9 119,8 230,4 114,7 92,6 123,3 Пол KKKMKKMMMKK Сальсолин 202,0 136,2 140,9 99,0 100 , 2 141,5 128,6 191,0 105,0 237,7 203,0 Секс ММККККККМК Сальсолин 300,5 170,1 161,9 179,8 254,0 355,0 397,0 375,0 378,0 252,0 - Пол MKKMMMMMMK - K-женщина, M-мужчина

Результаты испытаний t для этих данных показывают Рисунок 5

Как видите (результаты подчеркнуты линией), уровни значимости всех тестов на однородность дисперсии принимают значения менее 0,05. Поэтому мы должны отвергнуть нулевую гипотезу об однородности дисперсии. Поскольку предположение об однородности дисперсии не выполняется, мы учитываем значение критерия t для разнородных дисперсий (результаты выделены пунктирной линией). Из них следует, что уровень значимости принимает значение р = 0,0079. Поэтому можно сделать вывод, что существует значительная разница между средним уровнем сальсолина у мужчин и женщин. Графическая интерпретация полученных результатов показана на рисунке 6.

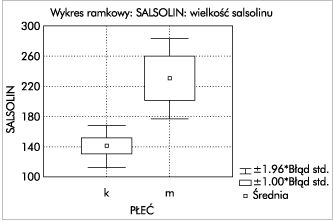
Рис. 6. Диаграмма «коробка с усами» - второй пример

В качестве последнего примера мы представляем результаты t- теста, сравнивающего количество лимфоцитов в двух группах пациентов. На этот раз р составляет 0,769 ( рисунок 7 ), поэтому у нас нет оснований отвергать нулевую гипотезу о равенстве средних.

Полученные различия могут быть результатом случайных ошибок. Это подтверждается ящиками с усами на рисунке 8.

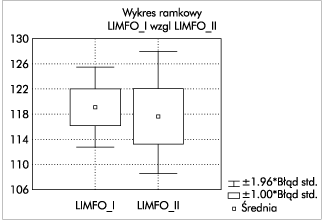
Рис. 8. Диаграмма "коробка с усами" - третий пример

Квадраты, представляющие среднее значение, находятся практически на одном уровне, и доверительный интервал (определяемый усами) для переменной LIMFO_I попадает в доверительный интервал переменной LIMFO_II.

В конце несколько слов о интерпретации результатов. Оценка статистического теста обычно проводится в форме предложения: «На заданном уровне значимости альфа = ... гипотеза нулевая H 0 ....... мы отвергаем или не имеем оснований отклонять его». Однако интерпретация результатов, полученных после проверки гипотез, является одним из наиболее сложных и важных этапов статистического анализа. Правильная интерпретация не может быть независимой от характера данных и способа их получения. «Сухих» чисел недостаточно. Лучше всего, если врач интерпретирует результаты вместе со статистиком. Давайте также помним, что статистический тест не доказывает истинность или ложность гипотезы. Результат статистического теста говорит только о вероятности истинности гипотезы и только в связи с правильно сформулированной альтернативной гипотезой. С помощью теста вы можете либо отклонить нулевую гипотезу, либо сказать, что результаты эксперимента не противоречат этой гипотезе. Непринятие нулевой гипотезы не равносильно ее принятию. «Нерелевантное» различие лучше всего рассматривать как «недоказанное». Возможно, например, увеличение размера выборочной группы покажет, что разница важна. Поэтому мы должны дать «отрицательный» результат вместе с доверительным интервалом. Следует также с осторожностью относиться к результатам с уровнем значимости, близким к 0,05.