Типы статистических характеристик Описательная статистика - показатели изменчивости, асимметрии и концентрации - Основы статистики - Связанные исследования - Статьи - Медицинская практика

В предыдущем эпизоде ​​мы узнали числа, описывающие «центр» набора данных. Эти цифры, однако, не дают полного изображения нашей коллекции. Например, в двух группах пациентов измеряли систолическое артериальное давление и были получены следующие результаты (в мм рт. Ст.):
- группа I: 145, 125, 130, 155, 140, 150, 135
- группа II: 115, 150, 100, 180, 140, 165, 130.

После выполнения расчетов выясняется, что среднее значение и медиана одинаковы в обеих группах и составляют 140 мм рт.

Однако, взглянув на эти данные, мы заметим, что значения во второй группе более рассеяны, чем в первой. Чтобы лучше понять наши данные, нам нужны «сводные» числа другого типа - показатели изменчивости (дисперсия, дисперсия). Вместе с описательной статистикой они дают очень краткое описание данных. Существует три типа показателей вариации: диапазон, дисперсия и стандартное отклонение.

Простейшей мерой изменчивости является диапазон (разница между самым высоким и самым низким результатом [R = xmax - xmin]). Однако это не идеальная мера. Легко представить две разные серии с одинаковыми диапазонами - выбросы могут привести к тому, что данные, сильно отличающиеся друг от друга, будут иметь одинаковые растяжки.

На практике чаще всего используются две меры: дисперсия и стандартное отклонение. Дисперсия переменной X называется средним арифметическим квадратов отклонений значений отдельных переменных от среднего арифметического всей совокупности.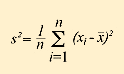

Это одно из важнейших понятий в статистике, и мы встретимся с ним практически во всех видах статистических выводов. Помните: чем больше дисперсия, тем больше разбросаны результаты наших измерений. Разделите всю группу в соответствии с определенными критериями на группы. Тогда дисперсия для всего населения (общая дисперсия) равна сумме двух компонентов: среднего арифметического значений внутригрупповых дисперсий значения переменной (дисперсии внутри группы) и дисперсии средних значений этой группы (дисперсии между группами). Это наблюдение является основой так называемого Дисперсионный анализ , часто определяемый аббревиатурой ANOVA (анализ риска).

Когда мы хотим получить меру вариации с титром, согласующимся с переменной, мы вычисляем квадратный корень из дисперсии, то есть так называемый стандартное отклонение (SD). * Стандартное отклонение находится рядом со средним значением наиболее часто используемого статистического параметра, который имеет следующие основные свойства:

1. Стандартное отклонение рассчитывается по всем результатам. Чем разнообразнее группа, тем выше стандартное отклонение. В представленных выше двух группах пациентов стандартные отклонения составляют: в первой - 10,8, а во второй - 27,83. Видно, что измерения во второй группе более рассеяны, чем в первой.

2. Стандартное отклонение соответствует правилу трех сигм (рис. 1), согласно которому в случае нормального или почти нормального распределения почти 31,73% всех результатов отличаются от среднего арифметического более чем на +/- SD;
только 5% наблюдений выходят за пределы диапазона ( 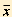- 2SD, 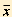+ 2SD);
только 0,3% всех наблюдений выходят за пределы диапазона ( 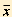- 3SD, 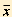+ 3SD).

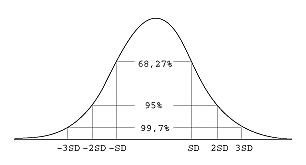
Рис. 1. Правило трех сигм

Обсуждаемые до сих пор показатели волатильности используются для определения абсолютной величины вариации в результатах нашего наблюдения и являются назначенными числами, а также описательной статистикой. Это создает трудности при сравнении вариаций в двух или более группах данных. Поэтому была введена новая мера, называемая коэффициентом вариации - это отношение стандартного отклонения к среднему арифметическому (V = SD / 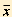х 100%). Для наших групп, в которых мы тестировали артериальное давление, коэффициенты вариации составляют 7,71% для первой группы и 19,88% (что почти в 2,5 раза выше) для второй группы.

Меры асимметрии
В некоторых ситуациях изучение среднего значения переменной и дисперсии значения переменной не указывает на наличие различий между исследуемыми сообществами, в то время как наблюдение за распределением этих признаков исключает сходство.

Пример: в трех группах по 100 человек время реакции на препарат было проверено. Данные представлены в виде таблицы.

Среднее арифметическое и дисперсия одинаковы для всех групп и составляют соответственно 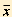= 35, s2 = 120. Однако есть большие различия, что хорошо видно на гистограммах на рисунок 2

Видно, что у большинства людей в группе 2 время реакции короче, а в группе 3 - больше среднего. Это связано с асимметрией распределения. Три ситуации встречаются рисунок 3 :

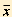= Me = Mo - симметричное распределение
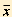> Me> Mo - разложение с правосторонней асимметрией
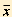<Me <Mo - распределение с левой асимметрией

Коэффициент асимметрии ( асимметрия ), символ - As был введен для определения направления и силы асимметрии. Этот коэффициент является ценным инструментом для статистического анализа. Сама средняя арифметика говорит мало. Только в связи с мерой изменчивости и мерой асимметрии мы получаем полную картину различий, которые существуют между рядами переменной. Коэффициент асимметрии, равный нулю, указывает на симметрию распределения переменной, положительное значение означает правостороннюю асимметрию (распределение имеет более длинный правый «хвост»), а отрицательное значение - левостороннюю асимметрию (распределение имеет более длинный левый «хвост»).

В нашем примере As для группы 1 равно 0 (симметричное распределение), для группы 2 - 0,2317 (правосторонняя асимметрия), а для группы 3. - -0,2317 (левосторонняя асимметрия).

Меры концентрации

Меры концентрации (концентрация) прекрасно дополняют ранее известные параметры. Они описывают концентрацию значения характеристики вокруг среднего.
Наиболее популярным показателем концентрации результатов вокруг среднего является куртоз ( kurtosis , K ). Чем выше значение K , тем тоньше числовая кривая и, следовательно, тем больше концентрация переменной вокруг среднего значения. Если K <0, распределение будет более плоским, чем обычно, а если K > 0 - более тонким (рисунок 4).

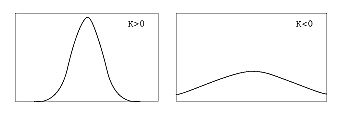
Рис. 4. Кривые обилия с другой мерой концентрации